Stellar masses are computed by multiplying a mass-to-light ratio M∕L with a luminosity L. While the uncertainties on L depend on the quality of the data, the estimate over M∕L and its associated uncertainties depend mostly on the care taken with SED fitting. It is a good idea to search fora reference band that minimizes the effects of M∕L variations due to stellar populations (age, metallicity, chemical abundances) and due to dust absorption. While the common notion that the NIR (e.g. the H band at 1.65 μm) is close to ideal is correct in some cases, problems can arise because of thermally pulsing asymptotic giant branch stars (discussed in section 2.1.3) if young ages (<2 Gyr) are well represented in the SED. That reliable M∕L from SED fitting cannot be dispensed with is evident when looking at IRAC 3.6μm data of nearby galaxies, where star formation regions are evidently prominent.
Stellar Mass Maps of Resolved Galaxies In the work of Zibetti, Charlot, and Rix (2009) a “data-cube” approach is introduced to investigate the SEDs of nearby, resolved galaxies, aimed at preserving the maximum spatially-resolved information. One feature of the approach is that it allows to compare “global” quantities, which are notoriously difficult to determine, with the integral over the local quantities, a useful test of how meaningful global quantities can be. A large part of the effort concentrated on developing a reliable method to obtain stellar surface mass density maps from a minimum set of broad-band observations. This method relies on Bayesian inference, as discussed in Section 4.5.
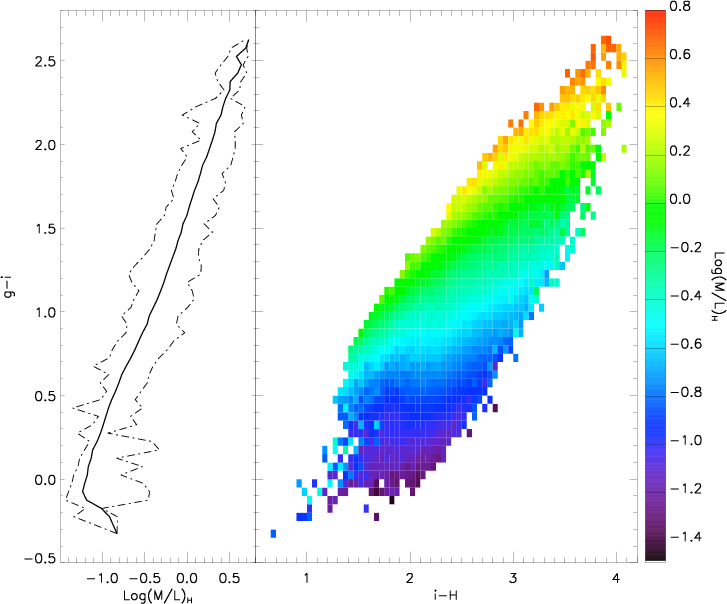
The effective mass-to-light ratio correlates with optical / near-infrared colors (e.g., Bell and de Jong 2001), so M∕L can be expressed as a function of color(s). A better estimate is obtained if M∕L is mapped as a function of two colors, instead of one. The colors adopted are g - i and i - H. Their large wavelength separation allows to robustly describe the shape of the SED over the entire optical-near-infrared range, in a way that as insensitive as possible to photometric and modeling uncertainties.
To study the dependence of M∕L on (g-i,i-H) the authors use a Monte Carlo library of 50,000 models created from the 2007 version of BC03, which include also dust in different amounts and spatial distributions.. The (g-i,i-H) space is binned in cells of 0.05 mag × 0.05 mag and marginalized over M∕L in each cell. The median is chosen as the fiducial M∕L at each position of the color-color space. A look-up table is created to derive M∕LH as a function of (g-i,i-H). Figure 23 illustrates that the information in the second color improves the M/L determinations systematically by ±0.3–0.4 dex.
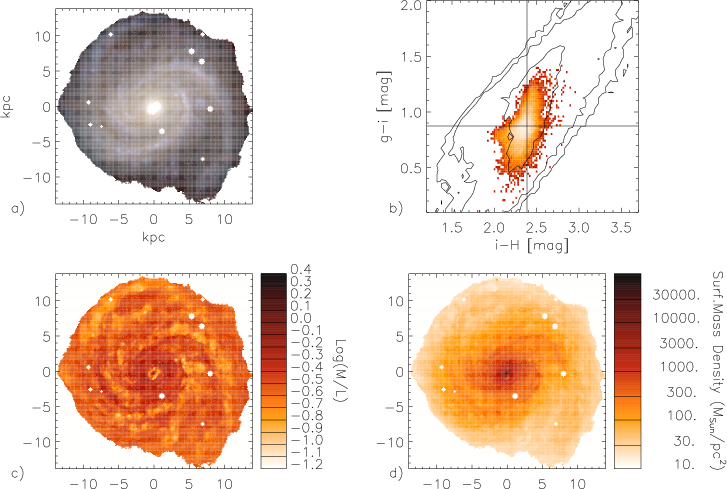
The method described above is applied to each pixel of the image of a galaxy, where “pixel” implies the pixel that results after matching the images in the three bands to a common resolution. In order to provide sensible results, it is crucial that color measurements do not exceed 0.1 mag errors, which requires S/N~20. The results for M 100 (NGC 4321) are displayed in Figure 24.
An important result appears from the comparison between total stellar mass as obtained by integrating the stellar mass surface density maps (Figure 24d) and the one obtained using global colors to estimate the “average” M∕L ratio to be multiplied by L(H). This second method, the one commonly adopted in extragalactic studies, agrees within ~10% of the mass map integral only when the color distribution is quite homogeneous, i.e., for early type galaxies. When substantial color inhomogeneities and especially heavily obscured regions are present within a galaxy, using global colors and fluxes can lead to underestimates of the actual stellar mass of a galaxy by up to 60%. This can be understood if dust-obscured regions can contribute a significant amount of mass but are heavily under-represented in the global color, which is flux weighted and hence biased toward the brightest (and bluest) parts of the galaxy. While the pixel-by-pixel M∕L gives the correct mass weight to these obscured regions, the globally computed M∕L severely underestimates their mass contribution.

Stellar mass functions One of the holy grails of current observational efforts in galaxy evolution studies is a consistent picture of the build-up of stellar mass over the age of the universe. An important constraint on this is the stellar mass function, or its integral, the stellar mass density. A comprehensive discussion of these results would warrant a review of its own. Suffice it here to point out that not only the local mass function has been measured with great precision (e.g. Bell et al. 2003a), but these results have also been extended to redshifts of 1 (Pozzetti et al. 2007; Bundy et al. 2006). At redshifts above 1.2 an observed-frame optical selection corresponds to a rest-frame UV selection, subject to large biases. These therefore have to be circumvented by a K-band selection (e.g. Cirasuolo et al. 2007) or, better, by a selection at 3.6μm (Arnouts et al. 2007; Ilbert et al. 2010, e.g.). For observational and conceptual reasons (detailed in Sections 4.5.2 and 4.6), determining stellar masses and therefore mass function at redshifts higher than z=2 is very difficult. Most authors thus prefer to restrict themselves to luminosity functions instead (see e.g. Cirasuolo et al. 2010, for just one very recent example), thus leaving the burden of transforming luminosities to stellar masses to the interpreting model (but see e.g. Kajisawa et al. 2009).
Stellar masses of high redshift galaxies Many authors have used some kind of Bayesian inference-based method (Section 4.5) to determine stellar masses for high redshift galaxies (e.g. Sawicki and Yee 1998; Papovich, Dickinson, and Ferguson 2001; Förster Schreiber et al. 2004). There is good hope that these mass estimates are reasonably good (Drory, Bender, and Hopp 2004), despite important caveats on the methodology that become more important with improving data quality (see e.g. Section 4.1). A recent result has been the discovery and study of high redshift galaxies with high stellar masses and low star formation rates (early type galaxies, ETGs). In the following we describe only one ”family” of papers, as presented at the workshop, but see Cimatti (2009) for a review. Massive ETGs are the first objects to populate the red sequence (see e.g. Kriek et al. 2008b). Objects in the redshift range 2-3 can be identified by multi-band photometry (e.g. van Dokkum et al. 2006). For determining the physical properties however, significant uncertainties are due to photometric redshift determinations. For example Kriek et al. (2008) conclude that while stellar masses are reasonably robust to small errors arising from photometric redshifts, the actual star formation history is generally very poorly constrained with broad band data alone.
The obvious next step is thus to analyze these galaxies with spectroscopy, despite this being an expensive undertaking in terms of telescope time. When doing this, Kriek et al. (2008) also go further in blurring the limits between spectroscopy and photometry by binning their “low” S/N spectra into bins of 400 Å. While the information content remains unchanged, this certainly leads to improvements in presentability and fitting speed. Kriek et al. (2009a) then show explicitly that provided enough photons can be assembled through either exposure time or telescope size, the spectra of galaxies at redshifts 2-3 are amenable to the same kind of analysis as in the local universe. The upshot of these studies is that massive, compact ETGs with very little residual star formation are in place already at redshifts between 2 and 3.
Despite these successes, the study of Muzzin et al. (2009a,b) confirms that even using spectroscopic data, model uncertainties mean that SED-derived stellar masses are affected with uncertainties of factors 2-3 at these redshifts. For further discussion on stellar mass determinations the reader is also referred to the review by de Jong & Bell (in prep.).
Comparing observations to semi-analytic models Trager and Somerville (2009) extend the semi-analytic model of Somerville et al. (2008) to predict the line absorption strengths (Section 4.2) of the resulting galaxies. This allows them to use the same analysis tools that would be used in the analysis of the measured line strengths of an observed sample of galaxies on objects with known properties, in particular star formation histories. They select in particular early type galaxies from the mock catalogues they produce and compute the index strengths of the resulting spectra. These index strengths can then be plotted on the same plots as real data. They come to the sobering conclusion that while the sample of Trager, Faber, and Dressler (2008) is of sufficient quality do do a meaningful comparison, it remains too small. On the other hand large samples of galaxies, as the one of Moore et al. (2002), still lack the required precision.
The archeology of the universe The database of the SDSS spectra has been used to derive the SFH of galaxies from their current spectra (e.g. Heavens et al. 2004, see also Section 4.4), a procedure sometimes called “unlocking the fossil record” or simply “astro-archeology”. A recent update on this has been presented in Tojeiro et al. (2007), who applied VESPA (see Section 4.4) to the SDSS sample of spectra and derived a catalogue that was made available to the community at http://www-wfau.roe.ac.uk/vespa/. It provides detailed star formation histories and other parameters for SDSS’s latest data release (DR7) of the Main Galaxy Sample and the Luminous Red Galaxies sample. Details of the catalogue, including description, basic properties and example queries can be found in (Tojeiro et al. 2009).
Combining spectroscopic and dynamic ages The use of spectroscopy in combination with dynamical arguments to understand the evolution of a single object was presented in Pappalardo et al. (2010). The galaxy NGC4388 is a member of the Virgo cluster and sports a huge trail of HI gas (Oosterloo and van Gorkom 2005). It represent an ideal study case for the effects of ram stripping on a galaxy moving in the intra-cluster medium (Vollmer and Huchtmeier 2003). The stripping age has been estimated to be of order 200 Myr from dynamical arguments. Using VLT/ FORS spectroscopy of the outer and inner regions of the galaxy and the STECKMAP program (Ocvirk et al. 2006), Pappalardo et al. (2010) were able to show that, while the inner region of the galaxy is of solar metallicity and has continued forming stars to the present day, the outer regions of the galaxy have sub-solar metallicity and have stopped forming stars roughly 200 Myrs ago, in accordance with the dynamical estimate. Single cases like this can thus help identify the processes and timescale associated with shutting down the star formation in galaxies, one of the most profound changes a galaxy can experience.
Star formation rates Star formation rates from SED fitting have been little used, with most authors preferring to rely on single tracers (see Section 4.5.3 for a comparison). Walcher et al. (2008) have used stellar masses and star formation rates consistently derived from the same SED fit to compare the predicted evolution of the stellar mass function to the observed one. The main result is that while stars form in blue cloud galaxies, most of the growth of the stellar mass function occurs in quiescent galaxies, in agreement with studies based on different tracers of star formation (e.g. Bell et al. 2007). From comparison with merger studies in the same field, Walcher et al. (2008) conclude that about half of the mass growth on the red sequence comes from major mergers and half from minor mergers.
Salim et al. (2007) have compared their SED-fitting SFRs to SFRs determined from emission lines. They find that some galaxies with no detected emission lines nevertheless have substantial SED-based SFRs. They attribute this result to “recent” star formation, i.e. stars that formed long enough ago that their emission lines already vanished, but still recently enough to be revealed in the galaxy SED. Recent HST imaging in the UV which clearly shows SF structures seems to confirm this (Salim & Rich 2010, ApJ submitted).
This is an underexplored use of SED fitting, in the opinion of the authors. One example, objects with differing SFR measurements from emission lines and SED fitting has been covered in the last section.
Finding Wolf-Rayet stars The availability of large databases of spectra, such as from the SDSS, and of accurate stellar population model predictions enables the search for rare objects or systematic deviations that are not predicted by the model itself. An example of this are Wolf-Rayet stars, evolved, massive stars with characteristic features. These have ages between 2 × 106 and 5 × 106 years, and are thus a transient feature of galaxy spectra. They are useful as a tracer of recent star formation history as well as the metallicity of their host galaxies. As shown in Brinchmann, Kunth, and Durret (2008), a systematic search in the SDSS database yields a sample several times larger than previous serendipitous searches. The essential ingredient of such a search is the accuracy of the stellar population model that allows an inversion technique (Section 4.4) to be applied on a large sample. Indeed, either a smooth correction or residual features from inaccurate models would severely impair the identification of the specific features. As an example Brinchmann, Kunth, and Durret (2008) show that the use of the Bruzual and Charlot (2003) models produced a large number of false positives, while an updated version of the same model using different stellar spectra (CB09) provides much better fits.