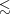10 Myr. These two measures, while
correlated, thus need to be properly corrected before being
able to compare them (see e.g. Kennicutt 1998; Boquien
et al. 2007; Kennicutt et al. 2009; Lee et al. 2009a, and
references therein).
In the context of a SED model, one must distinguish between independent, input parameters and derived parameters. Input parameters are those properties that are needed to define the SED model. Some of them may, first, not be measurable or, second, may not have a proper physical meaning by themselves. A good example for the first case is the shown in Figures 10 and 11 of da Cunha, Charlot, and Elbaz (2008), where the width of the probability distribution functions of different input parameters indicates which ones are well constrained, such as the global contribution of PAHs to the total luminosity, and which are not constrained, such as the temperature of warm dust in stellar birth clouds. Iglesias-Páramo et al. (2007, their Section 3) state another example, namely that only a few of the many input parameters of the GRASIL code need to be varied in order to produce a library of model spectra that cover a realistic range in observational properties. Further, more systematic study of the relative importance of the input parameters to dust emission models would seem to be a important addition to the literature. A good example of the second case is the “decay timescale”, τ*: in modelling the SEDs of early- and even late-type galaxies, the star formation histories (SFHs) are often represented as falling exponential functions modulated by this timescale, i.e. SFR(t) ∝ e(-t∕τ*). However, in a hierarchical universe the SFH is likely to be more stochastic in form, modulated by discrete accretion events. Thus the width of the falling exponential that one determines from an SED fit is a good measure of the mean age of the galaxy. It should by no means be assumed that this represents the true SFH of the galaxy. The reason that falling exponentials provide reasonable fits in practice is simply that the spectral features of SSPs vary smoothly with time and there is thus considerable degeneracy between the mass contributions of SSPs of different age, effectively smoothing the SFHs of galaxies. This smoothing makes it also impossible in practice to robustly disentangle the epoch of the formation of the most luminous stellar population in a galaxy from the timescale over which this star formation took place.
Input parameters constitute a discrete set with a
maximum number of members determined by the quality
of the data and the models. On the other hand the set of
derived parameters can be extended at will and not all
derived parameters can or need to be independent. For
example, the commonly used specific star formation
rate (sSFR= SFR∕M*) and the birthrate parameter
(b = SFR∕⟨SFR⟩t) are derived parameters that are very
similar. It is clearly relevant to properly define and
understand the derived physical properties that one
intends to measure. Let us again consider the SFR. While
the SFR derived from the UV flux traces an average SFR
over the last 100 Myr, the SFR determined from Balmer
emission lines measures the much shorter timescale of the
ionizing stellar flux, 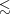10 Myr. These two measures, while
correlated, thus need to be properly corrected before being
able to compare them (see e.g. Kennicutt 1998; Boquien
et al. 2007; Kennicutt et al. 2009; Lee et al. 2009a, and
references therein).
As an integrated model of the optical SED of a galaxy is based more or less explicitly on an equation similar to Equation 1, the independent and derived parameters should be defined in the same terms (see e.g. Walcher et al. 2008, Table 1). Actually writing down the definition helps avoid common confusions (such as those between metallicity Z and [Fe/H], or concerning the time scale over which the SFR is measured) and should be considered good practice.