Principal Component Analysis

4.3 Principal Component Analysis

Fig. 10 : Comparison between the eigenspectra from a PCA of 2000 randomly selected SDSS galaxies: left, using a simple SVD algorithm, the first eigenspectrum is dominated by a single noisy galaxy spectrum; center, using sigma clipping to remove outliers iteratively from the dataset, the eigenspectra are visibly less noisy; right, a robust PCA of the dataset, now the distinct patterns in the dataset are strongly visible, in particular the separation of narrow nebular emission lines from broader photospheric absorption features. [Courtesy V. Wild]

Ideally we would like to represent a galaxy spectrum by a small set of continuous parameters that uniquely determine the best-fit spectrum. Principal Component Analysis (PCA) is one algorithm commonly used to derive an optimal set of linear components, diagonalising the covariance matrix of the data points to find the directions of greatest variation. Its representation of data through a linear combination of independent (orthogonal) components, or eigenvectors is thus an alternative method to using a set of discrete SSP templates (Section 4.4). Since the convolution with transmission curves is a linear operation, these methods are as simple as solving a linear equation, even for photometric datasets (Connolly et al. 1999; Budavári et al. 2000).

PCA has been successfully applied to astronomical spectral datasets, although not yet to photometric datasets which suffer the additional complication of observed-to-rest frame translation (Connolly et al. 1995b). The main difficulty with PCA is that the interpretation of the empirically determined PC components in terms of physical properties is complex at best (though see Wild et al. 2007, 2009; Rogers et al. 2007, 2010b). This is exacerbated by its sensitivity to outliers and hence out-of-the-box algorithms are of limited use for astronomical datasets.

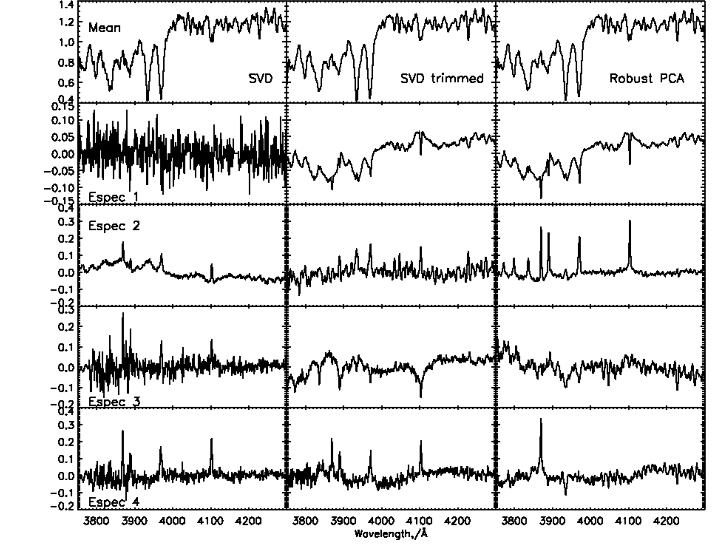
Recent work by Budavári et al. (2009b) solves the problem of reliable eigenspectra determination by an iterative procedure that is efficient to compute and robust in the statistical sense. Figure 10 illustrates the comparison of three PCA methods on the blue optical region of 2000 randomly selected SDSS galaxy spectra. Each column contains (from left to right) the results of the classic PCA, classic PCA using iterative sigma clipping of the dataset, and the new robust algorithm. What is immediately striking in the robust case is the following: (a) The very clean appearance of the nebular emission lines in the second eigenspectrum. (b) These are correlated with the weaker Balmer absorption (seen as broad wings on the narrow emission lines) and rise in the blue from the continua of O and B stars which are the dominant source of ionisation of the nebular emission lines. (c) The emission line in the 4th eigenspectrum is the only one in this wavelength range which is not a Balmer line, and with a higher ionisation state is sometimes attributed to the presence of an AGN. Without any prior physical knowledge, the robust PCA has separated out a line which is physically distinct from the others, and tied together HII emission lines with the O and B stars that excite them. The results are clearly of more use for characterising the galaxy population than traditional PCA algorithms. The robust PCA algorithm provides a new, fast and easy to use method for the investigation of real astronomical datasets in a model independent manner.

[next] [prev] [prev-tail] [front] [up]