Redshift errors are ultimately data-driven: they typically scale with 1 + z given constant wavelength resolution of most filter sets; they also scale with photometric error in a transition regime between ~ 2% and ~ 20%. Smaller errors are often not exploited due to mismatches between data and model arising from data calibration and choice of templates, while large errors translate non-linearly into weak redshift constraints. If medium-band resolution is available, QSOs show strong emission lines and lead to deeper photo-z completeness for QSOs than for galaxies.
Photometric redshifts have limitations they share with spectroscopic ones, and some that are unique to them: as in spectroscopy, catastrophic outliers can result from the confusion of features, and completeness depends on SED type and magnitude. Two characteristic photo-z problems are mean biases in the redshift estimation and large and/or badly determined scatter in the redshift errors. Catastrophic outliers result from ambiguities in colour space: these are either apparent in the model and allow flagging objects as uncertain, or are not visible in the model but present in reality, in which case the large error is inevitable even for unflagged sources. Empirical models may be too small to show local ambiguities with large density ratios, and template models may lack some SEDs present in the real Universe.
Remedies to these issues include adding more discriminating data, improving the match between data and models as well as the model priors, and taking care with measuring the photometry and its errors correctly in the first place. Photo-z errors in broad-band surveys appear limited to a redshift resolution near 0.02 × (1 + z), a result of limited spectral resolution and intrinsic variety in spectral properties. Tracing features with higher resolution increases redshift accuracy all the way to actual spectroscopy. Future work among photo-z developers will likely focus on two areas: (i) Understanding the diversity of codes and refining their performance; and (ii) Describing photo-z issues quantitatively such that requirements on performance and scientific value can be translated into requirements for photometric data, for the properties of the models and for the output of the codes.

In general, template-based photo-z estimates depend sensitively on the set of templates in use. In particular, it has been found that better photo-z estimates can be achieved with an empirical set of templates (e.g. Coleman, Wu, and Weedman 1980; Kinney et al. 1996) rather than using stellar population synthesis models (SPSs; e.g. Bruzual and Charlot 2003; Maraston 2005, see Section 2) directly. Yet the models are what are commonly used to compute stellar masses of galaxies. Since the use of these templates do not result in very good photometric redshifts, what is usually done, is to first derive photometric redshifts through empirical templates, and then estimate the stellar masses with the SSP templates. Obviously this is not self-consistent.
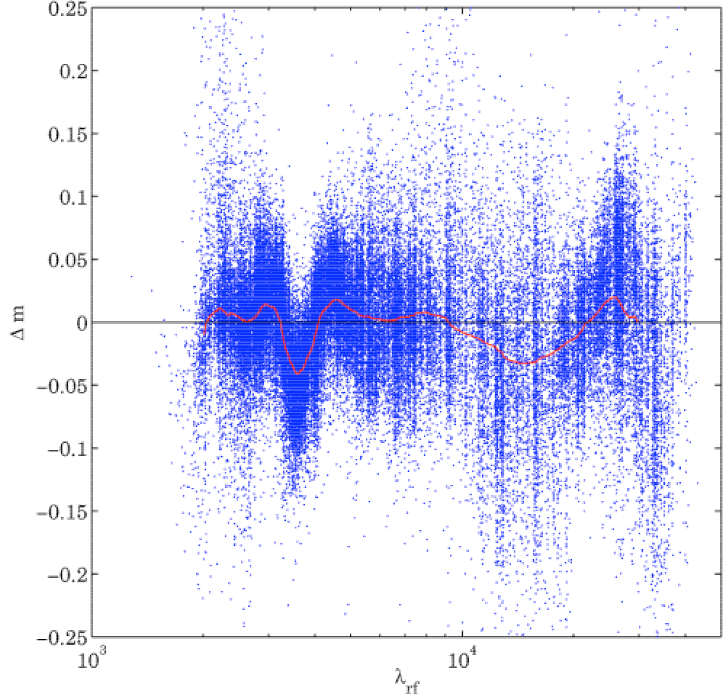
To investigate what causes the poorer photo-z estimates of synthetic templates, Oesch et al. (in prep.) used the photometric data in 11 bands of the COSMOS survey (Scoville et al. 2007), together with redshifts of the zCOSMOS follow-up (Lilly et al. 2007) and fit the data with SSP templates. In the resulting rest-frame residuals they identified a remarkable feature around 3500 Å, where the templates are too faint with respect to the photometric data, which can be seen in figure 17. The feature does not seem to be caused by nebular continuum or line emission, which they subsequently added to the original SSP templates. Additionally, all types of galaxies suffer from the same problem, independent of their star-formation rate, mass, age, or dust content.
Similar discrepancies have been found previously by Wild et al. (2007); Walcher et al. (2008), who found a ~ 0.1 mag offset in the Dn(4000) index. As this spectral break is one of the main features in the spectrum of any galaxy, it is likely that the poor photo-z performance of synthetic templates is caused by this discrepancy. The cause of the discrepancy has been identified as a lack of coverage in the synthetic stellar libraries used for the models. It will thus be remedied in the next version of GALAXEV (G. Bruzual, priv. comm.).
One of the strong benefits of the template method is that any spectroscopic subsample of a survey can be used to check the template-determined photo-zs. This can also be done for the empirical methods, yet for this a very large spectroscopic sample is necessary such that it can be divided into a large enough training set and testing sets.
With the existence of a test spectroscopic sample, it is then possible to calibrate the template library, leading to acombined empirical-template method. This means to correct for errors in the photometric calibration or even the correction of the templates themselves for example to allow for the evolution of galaxies with a small library, or to account for inaccurate models (see section 2). Such calibration is typically an iterative process, in which the photometry and/or template SEDs are modified to minimize the dispersion in the resulting photometric redshifts.
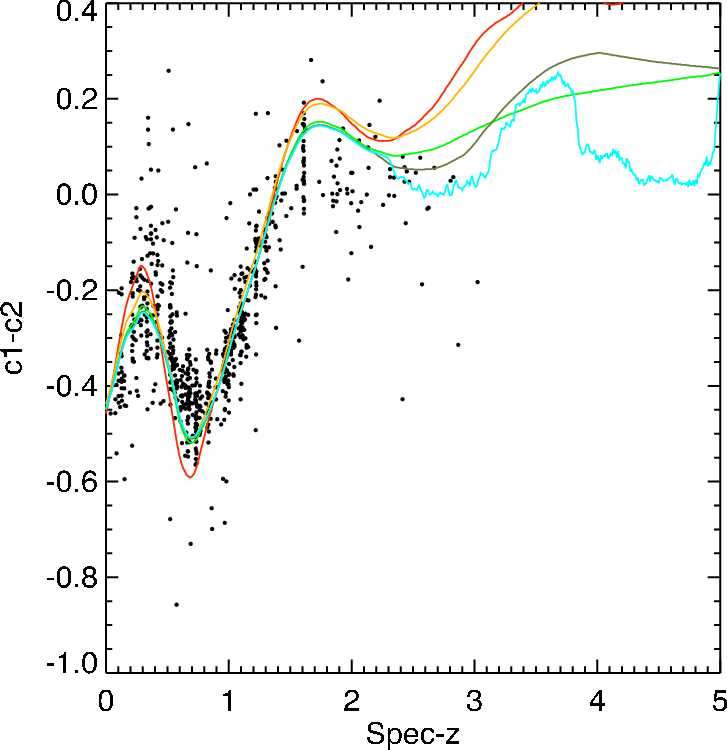
The simplest kind of calibration involves adding small zero-point offsets to the photometry uniformly across the sample. This does not imply that the photometry is incorrectly calibrated (though in practice the absolute calibration may well have small errors in the zero-point), but rather that there is often a mismatch between the real SEDs of galaxies and the templates used to fit them. The calibration is meant to minimize those differences. Plotting color-color or color-redshift diagrams (figure 18) with the template SEDs overlaid will often indicate bulk offsets between the two.
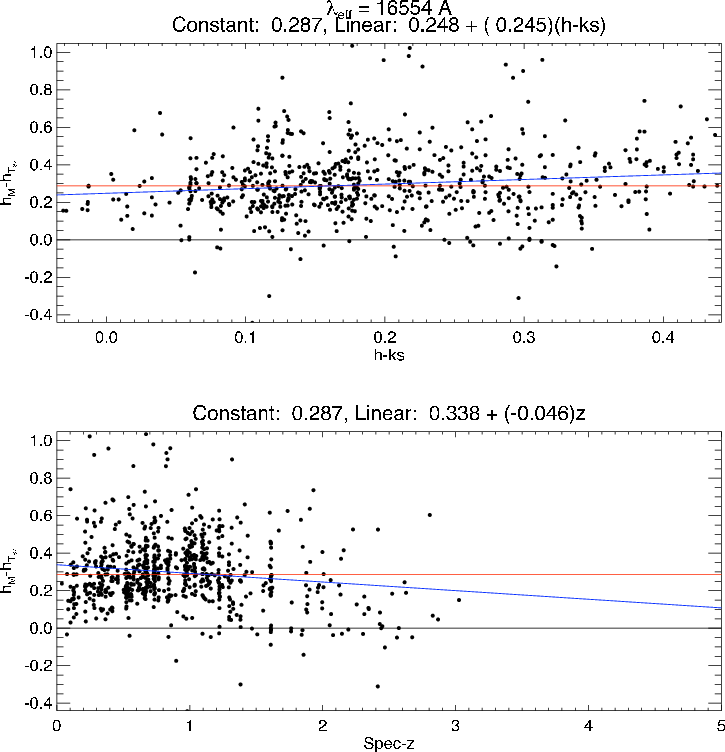
A more instructive approach, however, is to compute the residuals between the predicted magnitude of the best-fit template at the spectroscopic redshift and the observed magnitude (for more details, see Brodwin et al. 2006a,b). These residuals can be plotted versus color or redshift for added diagnostic power. In the example in Figure 19, there appears to be an effective magnitude offset of ≈ 0.3 mags in the H-band.
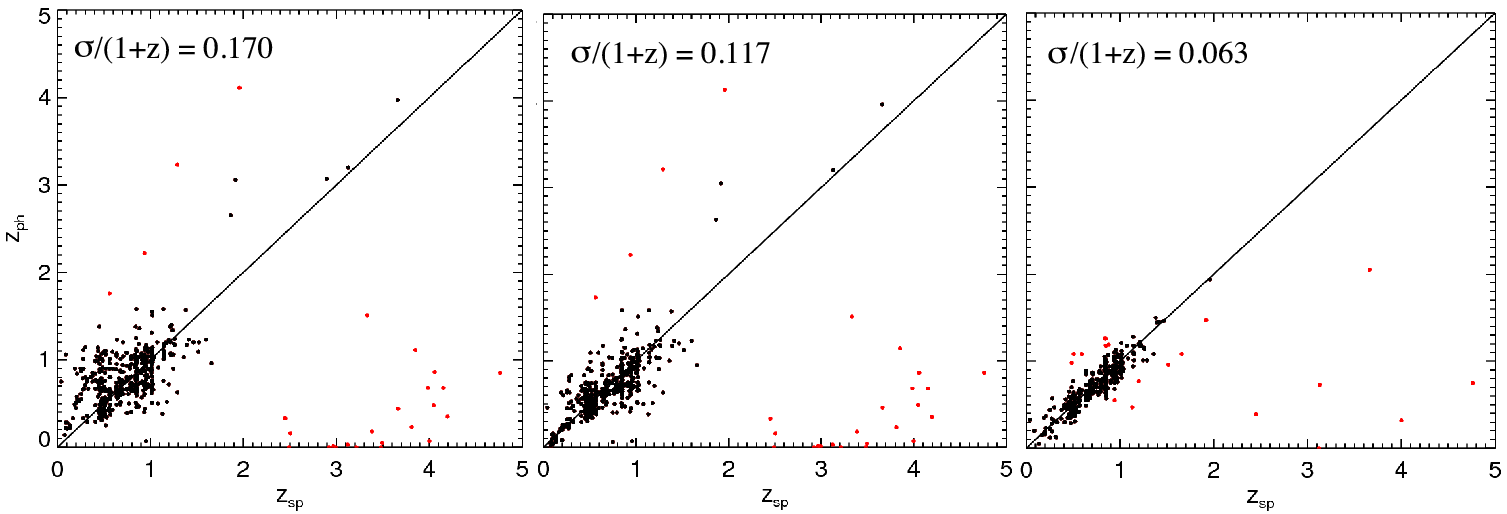
Applying such effective zero-point adjustments in all bands in an iterative process minimizes the mismatch between the data and the templates, and hence minimizes the resultant photometric redshift dispersion, as shown in Fig. 20.
Such calibration phases are used in the works of Brodwin et al. (2006a) and as “template-optimization” in the codes zebra (Feldmann et al. 2006) and Le Phare (Ilbert et al. 2006, 2009a) which use template fitting with Bayesian inferences and this calibration phase to give the most accurate photometric redshifts possible with the template approach.
With the most accurate photometric redshifts possible, the template-fitting can then be used to estimate physical properties such as stellar masses, star-formation rates, etc. (see section 6).
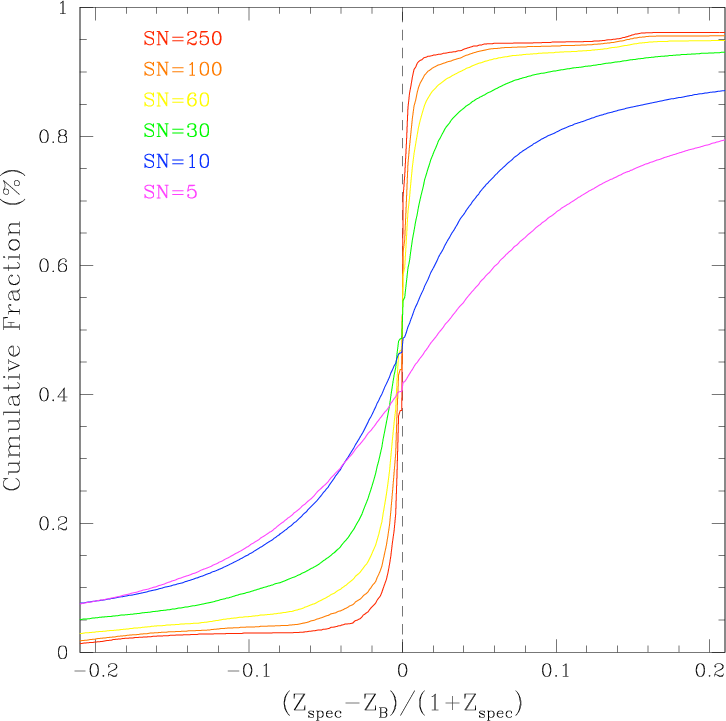
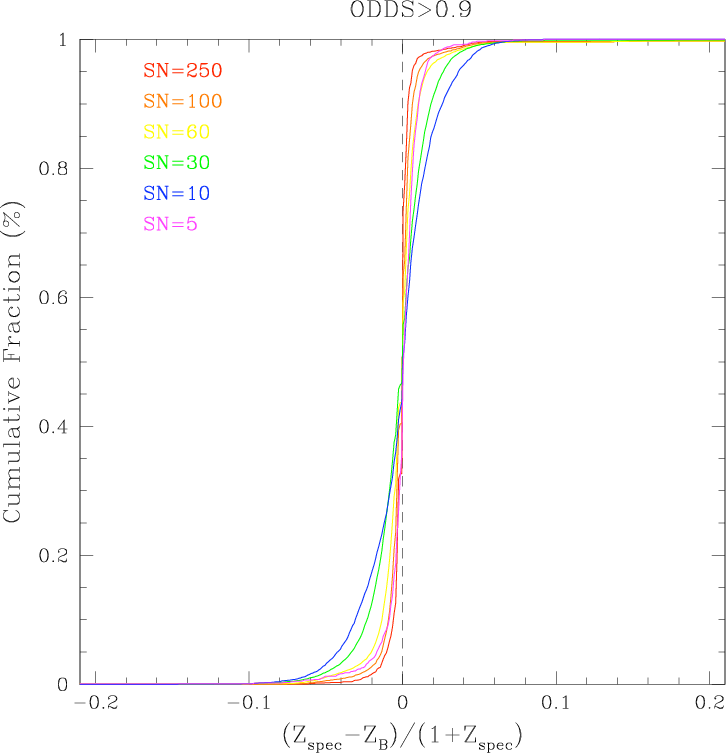
Margoniner and Wittman (2008) have specifically investigated the impact of photometric signal-to-noise (SN) on the precision of photometric redshifts in multi-band imaging surveys. Using simulations of galaxy surveys with redshift distributions (peaking at z ~ 0.6) that mimics what is expected for a deep (10-sigma R band = 24.5 magnitudes) imaging survey such as the Deep Lens Survey (Wittman et al. 2002) they investigate the effect of degrading the SN on the photometric redshifts determined by several publicly available codes (ANNz, BPZ, hyperz)
Figure 21 shows the results of one set of their simulations for which they degraded the initially perfect photometry to successively lower SN. In these unrealistic simulations all galaxies have the same SN in all bands. The figure shows the cumulative fraction of objects with δz smaller than a given value as a function of δz. The left panel shows the cumulative fraction for all objects, while the right panel shows galaxies for which the BPZ photo-z quality parameter, ODDS > 0.9. The number of galaxies in the right panel becomes successively smaller than the number in the left as the signal-to-noise decreases (64% of SN=250, and only 6.4% of SN=10 objects have ODDS > 0.9), but the accuracy of photo-zs is clearly better.
The results of this work show (1) the need to include realistic photometric errors when forecasting photo-zs performance; (2) that estimating photo-zs performance from higher SN spectroscopic objects will lead to overly optimistic results.