
The field of photometric redshifts and the estimation of other physical properties has been very pragmatic. Its development, since the first attempts, has been incremental in the sense that most studies focused on refining components but staying within the concepts of the original ideas of the two classes. Empirical and template-fitting approaches today follow very separate routes, with these classes of methods even use different sets of measurements. Only the semi-empirical approach of zero-point calibration comes close to linking the two approaches. However, a recent study by Budavári (2009a), tries to understand this separation and possibly bring these methods together by devising a unified framework for a rigorous solution based on first principles and Bayesian statistics.
This work starts with a minimal set of requirements: a training set with some photometric observables x and spectroscopic measurements ξ, and a query or test set with some potentially different set of observables y. The link between these is a model M that provides the mapping between x and y, the probability density p(x|y,M). This is more than just the usual conversion formula between photometric systems because it also incorporates the uncertainties.
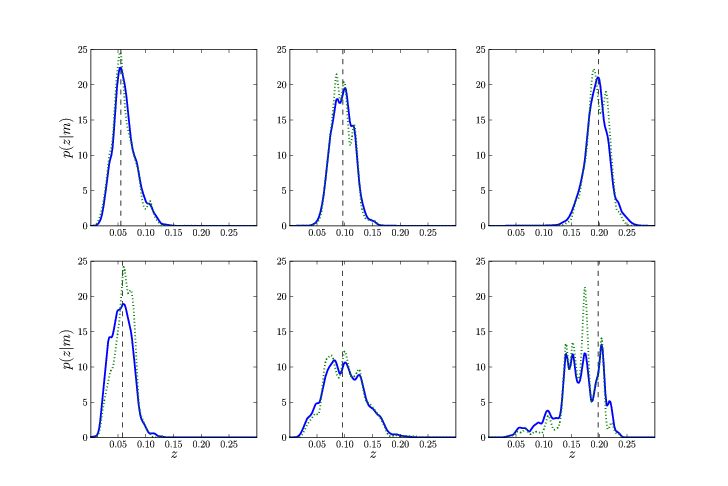
The empirical relation of x-ξ is often assumed to be a function. A better approach is to leave it general by measuring the conditional density function. The simplest way is to estimate the relation by the densities on the training set as p(ξ|x) = p(ξ,x)∕p(x). The final result is just a convolution of the mapping and the measured relation: p(ξ |y , M) = ∫ dxp(ξ|x)p(x|y,M). In figure 22 we show the results from Budavári (2009a), where he plots the empirical relation (dotted blue line) and the final probability density (solid red) for a handful of SDSS galaxies. The top panels show intrinsically red galaxies, whose constraints are reasonably tight out to the highest redshifts. Blue galaxies in the bottom panels however get worse with the distance as expected.
The aforementioned application follows a minimalist empirical approach but already goes beyond traditional methods. Template-fitting is in the other extreme of the framework where the training set is generated from the model using some grid. Without errors on the templates, the equations reduce to the usual maximum likelihood estimation that is currently used by most codes. A straight forward extension Budavári (2009a) suggests is to include more realistic errors for the templates. Similarly one can develop more sophisticated predictors that leverage existing training sets and spectrum models at the same time.